Coding Identity Matrix in Python
Implementing an algorithm for finding an identity matrix.
Filter by Category
Filter by Author

Implementing an algorithm for finding an identity matrix.
Basically, the identity matrix is a matrix of zero elements except for the main diagonal elements is set to one. a more formal definition could be written as
A matrix I ∈ R equals the n × n identity matrix if all its elements equal zero, except for the elements on the diagonal, which all equal one.
But before we drill deep let’s answer these…
How to represent a matrix programmatically in python?
we do that simply by considering the matrix as an array of arrays (an array that contains nested arrays). In which each nested array represents a row of the matrix.
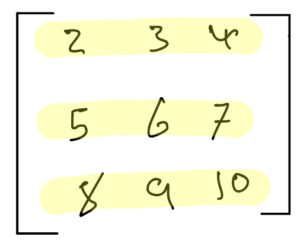
So that could be written as
array = [[2,3,4],[5,6,7],[8,9,10]]Meanwhile, the objective is getting the identity matrix for any given n x n matrix. taking the above matrix as example. The identity matrix should be
arrayIdentity = [[1,0,0],[0,1,0],[0,01]]They could be many ways to achieve that programmatically But, the approach we’re taking here is to go through a matrix column by column. Each time as we are marching through the matrix we slice every column into two arrays setting the first array to array of zeros and the second array to also zeros except for the first element.
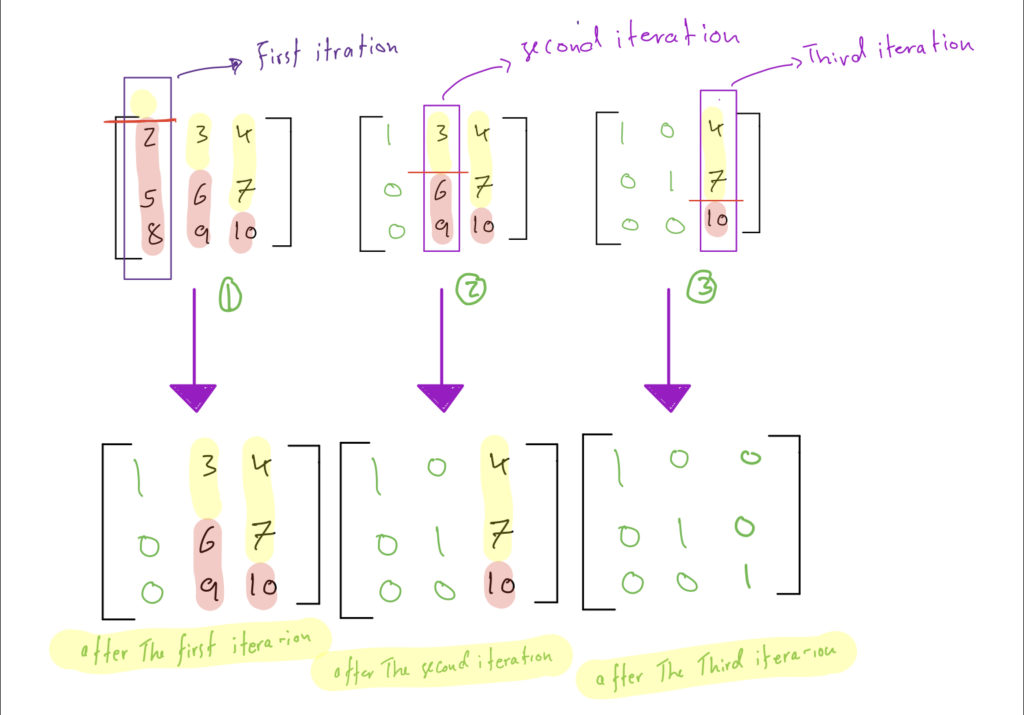
The algorithmic steps for finding identity matrix
First iteration
1- taking the first column.
2- split into two arrays however, the size of the first array determine by the iteration order. so we start by zero-size array and increment by one on each iteration.
so we end up with
iterationArrayA = []
iterationArrayB = [2,5,8]3- set the first array to zeros if it has elements. And the second array to zeros except for the first element.
iterationArrayA = []
iterationArrayB = [1,0,0]4- concat both arrays.
firstIterationArray = iterationArrayA + iterationArrayB = [1,0,0]
Second iteration
1- taking the first column.
2- split into two arrays however, the size of the first array determine by the iteration order. so we start by zero-size array and increment by one on each iteration.
so we end up with
iterationArrayA = [3]
iterationArrayB = [6,9]3- set the first array to zeros if it has elements. And the second array to zeros except for the first element.
iterationArrayA = [0]
iterationArrayB = [1,0]4- concatenate both arrays.
secondIterationArray = iterationArrayA + iterationArrayB = [0,1,0]
Likewise, steps are similar for the Third iteration as well as for any n x n matrix.
Now, all we have to do is to concatenate the final arrays of each iteration, then we end up with an identity matrix.
identityMatrix = firstIterationArray + secondIterationArray + thirdIterationArray
# result: [[1,0,0],[0,1,0],[0,0,1]]That’s all fine… translating that to code is our next challenge. For starters let’s build some handy functions that will break our problem into smaller pieces then we tackle them one at a time.
The first set of these functions is one that returns an array of all the columns for a given matrix (The matrix transpose ). Remember our matrix is stored in an array of arrays like structure, each inner array represents a row of a matrix, so there is a bit of work needs to be done here, in order to get the column arrays (The matrix transpose).
so below is how we can find the matrix transpose in python.
# loop though a matrix only return a single column given by its index
def getColumn(matrix, col):
try:
return [y[col] for y in matrix]
except:
return []
# loop through an array returning all its column arrays
def transpose(matrix):
result = []
numberOfCol = len(matrix)
numberOfRow = len(matrix[0])
numOfIteration = numberOfCol > numberOfRow and numberOfCol or numberOfRow
for index in range(numOfIteration):
if(len(getColumn(matrix, index)) > 0):
result.append(getColumn(matrix, index))
return result
Our next handy function is a scale function which takes any matrix or an array and scale it by a certain value, that will become useful when we want to find a zeros array.
# check if a given value matrix or an array
def isMatrix(vect):
try:
return type(vect[0]) is list
except:
return False
def scale(vect, alpha):
result = []
if(isMatrix(vect)):
for elm in vect:
scalledElm = [x * alpha for x in elm]
result.append(scalledElm)
return result
else:
return [i * alpha for i in vect]Great! that you make it these far. In addition, to our handy functions let’s build another two functions first one will returns a matrix of zero elements for any given matrix which is simply a subroutine that calls our scale() function with a scale value set to zero.
The second function is one that returns a matrix of zeros elements for any given matrix except for the first element set to one.
##### PART C #####
# check whether argument is matrix or an array
# if its an array simply set the first element to One
# if its matrix set the first element of the first nested array to One
def setElmOneElseZero(vect):
zeroMatrix = setAllElmToZero(vect)
if not(isMatrix(vect)):
zeroMatrix[0] = 1
return zeroMatrix
zeroMatrix[0][0] = 1
return zeroMatrix
# set each element of given array 'vect' to zero
def setAllElmToZero(vect):
zeroMatrix = scale(vect, 0)
return zeroMatrix
finally, we’ve all our tools ready for implementing the matrix identity algorithm.
moreover, we’ll implement that in steps, First of which is to define new functions
that’ll take column array and index, then slice the column array into two arrays then sets the first array to zeros array using the function setAllElmToZero().
In addition we pass the second array to the function setElmOneElseZero() which will set the first element to one.
##### PART D #####
def columnSlicing(vect, index):
if(index >= len(vect)):
raise Exception("\n >> Error! Invalid index")
vectSubA = vect[:index]
vectSubB = vect[index:]
vectA = []
# if vectSubA is empty(that's true in the first iteration)
# then no need todo any operation on it
if(len(vectSubA) > 0):
vectA = setAllElmToZero(vectSubA)
vectB = setElmOneElseZero(vectSubB)
return vectA+vectBThen the capstone step will be to enumerate through our original matrix. passing each column array to the subroutine columnSlicing() and we’re Done ✅
##### PART F #####
def identityMatrix(vect):
result = []
columnsArray = transpose(vect)
for index, columnVect in enumerate(columnsArray):
subArray = columnSlicing(columnVect, index)
result.append(subArray)
# rotating back to original matrix dimensions
identityMtrx = transpose(result)
return identityMtrx

So this article is about validating a fun logic game called sudoku. Sudoku board is consists of 9×9 gird, which contains 3×3 subgrids.The objective is to fill a 9×9 grid...

Login to your elastic compute instance with a private-key each time isn’t quite convenient. So we will change that by creating a new user, set ssh config and enabling...