React Suspense And Fetching Approach
How React suspense work, How to trigger the suspense fallback manually
Filter by Category
Filter by Author

How React suspense work, How to trigger the suspense fallback manually
Posted by Baraa Abuzaid

How to validate Sudoku board and check the input correctness programatically.
Posted by Baraa Abuzaid

Creating a new user on EC2 instance and access it remotely via ssh.
Posted by Baraa Abuzaid

How to fix React native ./gradlew access error
Posted by Baraa Abuzaid

Implementing an algorithm for finding an identity matrix.
Posted by Baraa Abuzaid

How React suspense work, How to trigger the suspense fallback manually
When it comes to fetching and rendering content in a React App, there are a few key strategies to consider: Fetch on render, Fetch then render, fetch as you render. Of these, the most effective approach is Fetch as You Render, which has been made possible thanks to the introduction of React Suspense. By utilizing Suspense, your components can patiently await async operations as they are dynamically rendered on the screen. This allows you to clearly express loading state declaratively and eliminate any potential race conditions.
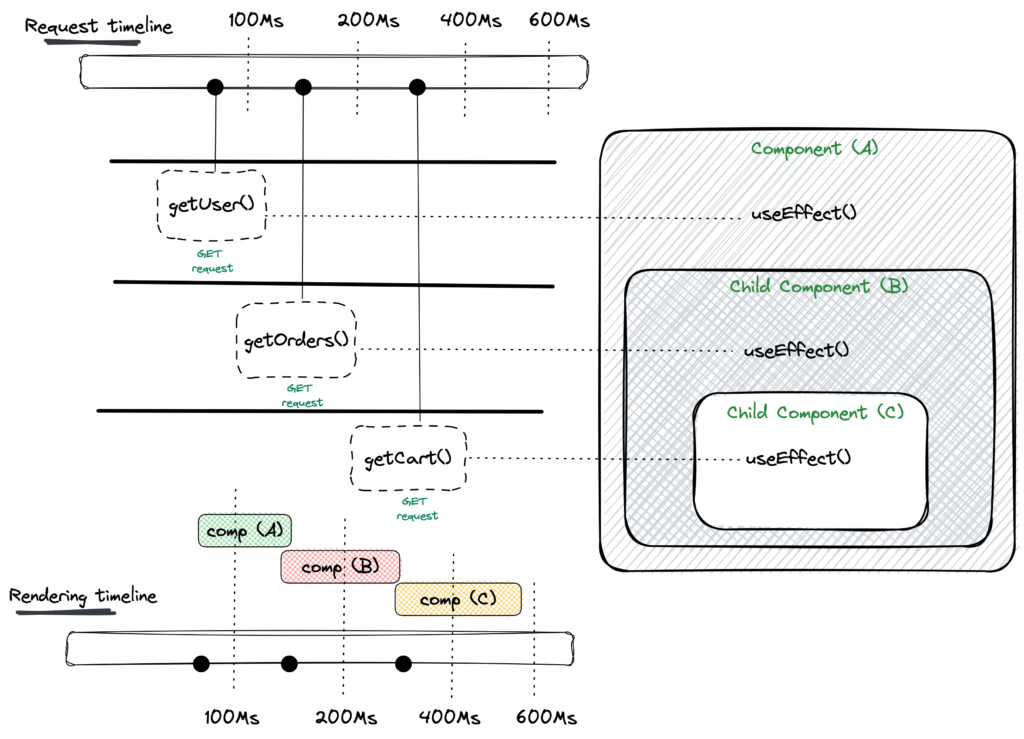
This is known as waterfall. Each competent won’t start fetching data until its parent request resolve. This because fetching only start after the component render on the screen.
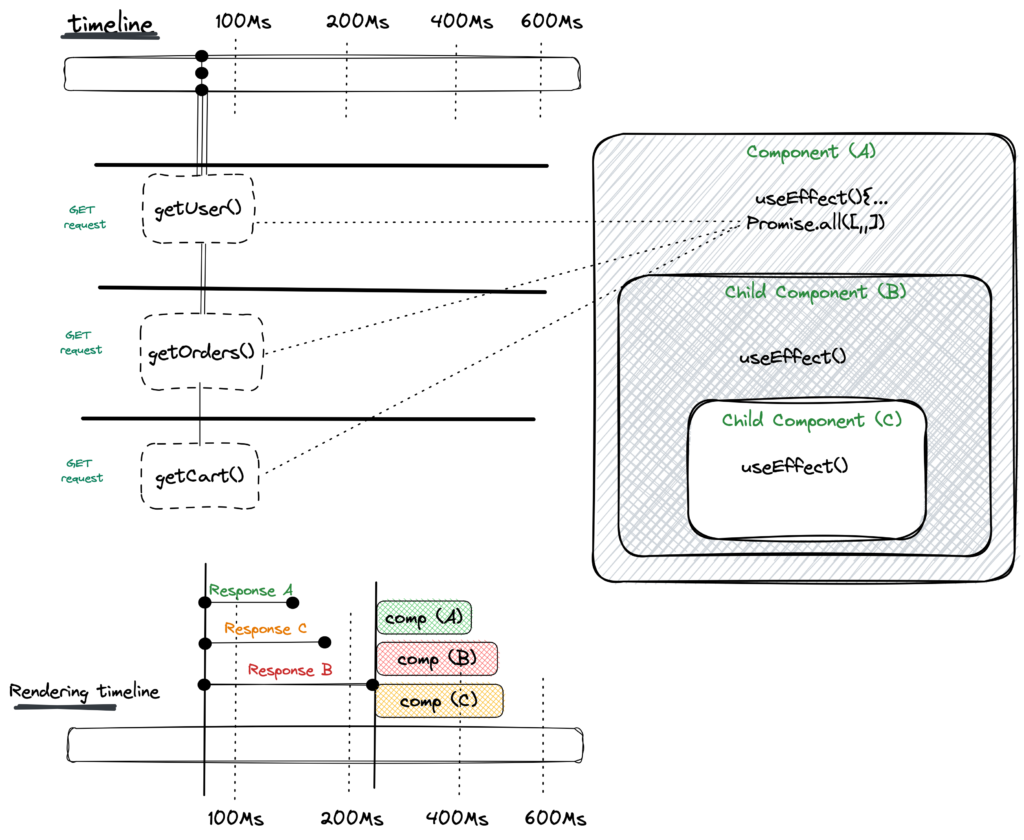
Unlike fetch-on-render, we managed to send all our requests in parallel and avoid having to wait before sending each request, nevertheless with promise.all we are bottleneck by our longest query. Thus, waiting for all requests to resolve before starting with any render.
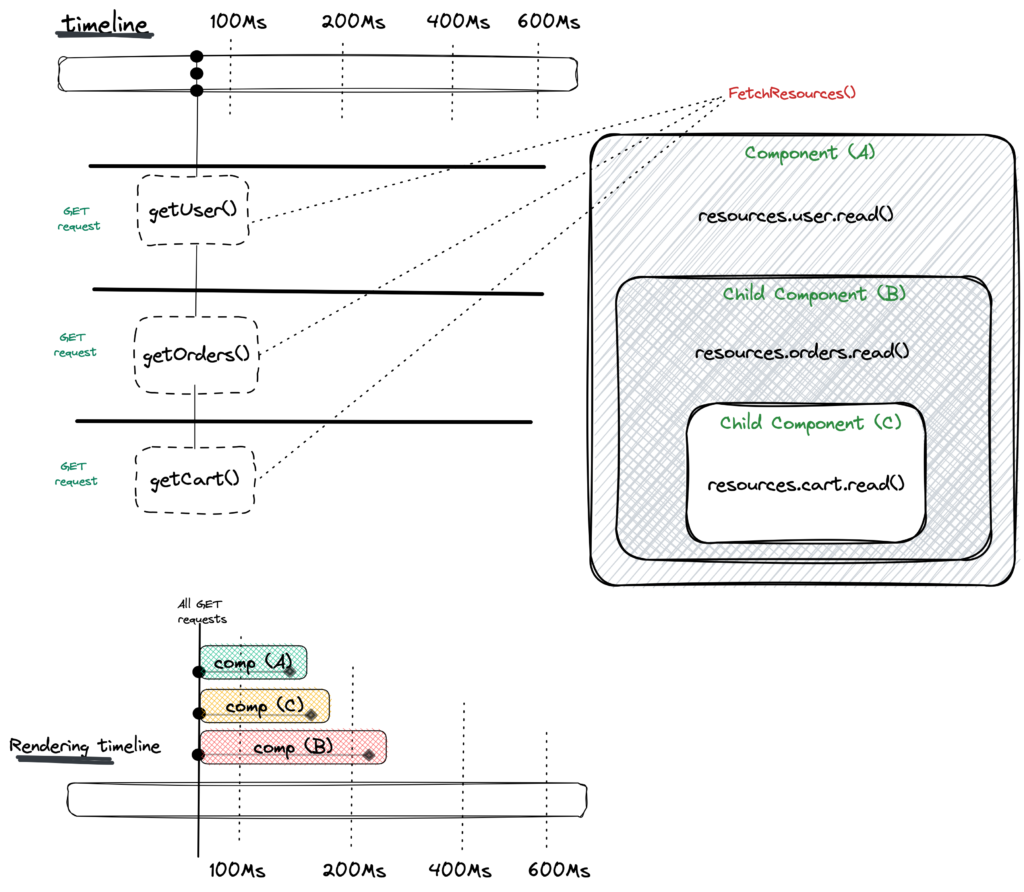
With render-as-you-fetch implemented with help of Suspense we don’t wait for the response. We can can start rendering immediately.
If you are using any fetching library like Relay or React Query. You would see that by wrapping your component with a Suspense, it magically fall into loading state whenever the component start to make a fetch.
What have happened internally is that during loading state the fetching library throws unresolved promise to trigger the Suspense state (loading state) in React.
to make this happen we can create a helper function, and call it a promise wrapper, that take a promise as an argument and resolved on request success or throw a promise while it is on pending state.
// resources.ts
type WrapPromiseReturn<T> = {
read: () => T | never;
};
const wrapPromise = <T extends Record<string,never>,>(promise: Promise<T>): WrapPromiseReturn<T> => {
let status: 'pending' | 'error' | 'success' = 'pending';
let result= {};
const suspender = promise
.then((data) => {
result = data;
status = 'success';
})
.catch((error) => {
result = error;
status = 'error';
});
return {
read(): T {
if (status === 'pending') throw suspender;
else if (status === 'error') throw result;
else return result as T;
},
};
};We can stub out some fake api requests to use with wrapPromise
// resources.ts
const getUser = (): Promise<string> =>
new Promise(resolve => setTimeout(() => resolve('Fake User 1'), 10800));
const getOrders = (): Promise<string[]> =>
new Promise(resolve =>
setTimeout(() => resolve(['Fake order 1', 'Fake order 2']), 8000),
);
const getCart = (): Promise<string> =>
new Promise(resolve => setTimeout(() => resolve('Fake item on cart'), 1000));
type WrapPromiseReturn<T> = {
read(): T;
};Let’s create our resources using wrapPromise.
// resources.ts
export const getResources = () => {
return {
user: wrapPromise(getUser()),
orders: wrapPromise(getOrders()),
cart: wrapPromise(getCart()),
};
};Using this will be as easy as importing it.
import React from 'react';
import {Text, View, StyleSheet} from 'react-native';
import {getResources} from './resources';
const resources = getResources();
export const UserProfile: React.FC<{}> = () => {
return (
<>
<View>
<Text style={style.title}>User Profile</Text>
<Text style={style.text}>{resources.user.read()}</Text>
</View>
</>
);
};
export const OrdersView: React.FC<{}> = () => {
return (
<>
<View>
<Text style={style.title}>My Orders</Text>
<View>
{resources.orders.read().map(item => (
<Text style={style.text}>{item}</Text>
))}
</View>
</View>
</>
);
};
export const CartView: React.FC<{}> = () => {
return (
<View>
<Text style={style.title}>My Cart</Text>
<Text style={style.text}>{resources.cart.read()}</Text>
</View>
);
};
const style = StyleSheet.create({
title: {
fontSize: 22,
fontWeight: '800',
color: 'tomato',
},
text: {
fontSize: 14,
fontWeight: '400',
},
});
import {CartView, OrdersView, UserProfile} from './src/components';
const App = (): JSX.Element => {
return (
<ScrollView>
<Suspense fallback={<Text>Loading User...</Text>}>
<UserProfile />
</Suspense>
<Suspense fallback={<Text>Loading Orders...</Text>}>
<OrdersView />
</Suspense>
<Suspense fallback={<Text>Loading Cart...</Text>}>
<CartView />
</Suspense>
</ScrollView>
);
};Fetch as you render is the best approach because we kickoff all our requests early with
resources = getResources(); yet we didn’t wait for the response to start rendering. Meanwhile, we rely on React to suspense then retry rendering our component as the data streamed back from our initial request.

So this article is about validating a fun logic game called sudoku. Sudoku board is consists of 9×9 gird, which contains 3×3 subgrids.The objective is to fill a 9×9 grid...

If you are getting this error and you are pulling your hair off try to figure out what goes wrong! look no further here are few steps you can take to solve this issue. error...